Leetcode|排序

图解算法数据结构 - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台 (leetcode-cn.com)

排序算法简介⁍

概述⁍

排序算法用作实现列表的排序，列表元素可以是整数，也可以是浮点数、字符串等其他数据类型。生活中有许多需要排序算法的场景，例如：

• 整数排序： 对于一个整数数组，我们希望将所有数字从小到大排序；
• 字符串排序： 对于一个姓名列表，我们希望将所有单词按照字符先后排序；
• 自定义排序： 对于任意一个 已定义比较规则 的集合，我们希望将其按规则排序；

同时，某些算法需要在排序算法的基础上使用（即在排序数组上运行），例如：

• 二分查找： 根据数组已排序的特性，才能每轮确定排除两部分中的哪一部分；
• 双指针： 例如合并两个排序链表，根据已排序特性，才能通过双指针移动在线性时间内将其合并为一个排序链表。

接下来，本文将从「常见排序算法」、「分类方法」、「时间与空间复杂度」三方面入手，简要介绍排序算法。「各排序算法详细介绍」请见后续专栏文章。

常见算法⁍

常见排序算法包括「冒泡排序」、「插入排序」、「选择排序」、「快速排序」、「归并排序」、「堆排序」、「基数排序」、「桶排序」。如下图所示，为各排序算法的核心特性与时空复杂度总结。

如下图所示，为在 「随机乱序」、「接近有序」、「完全倒序」、「少数独特」四类输入数据下，各常见排序算法的排序过程。

分类方法⁍

排序算法主要可根据 稳定性 、就地性 、自适应性 分类。理想的排序算法具有以下特性：

• 具有稳定性，即相等元素的相对位置不变化；
• 具有就地性，即不使用额外的辅助空间；
• 具有自适应性，即时间复杂度受元素分布影响；

特别地，任意排序算法都 不同时具有以上所有特性 。因此，排序算法的选型使用取决于具体的列表类型、元素数量、元素分布情况等应用场景特点。

稳定性：⁍

根据 相等元素 在数组中的 相对顺序 是否被改变，排序算法可分为「稳定排序」和「非稳定排序」两类。

• 「稳定排序」在完成排序后，不改变 相等元素在数组中的相对顺序。例如：冒泡排序、插入排序、归并排序、基数排序、桶排序。
• 「非稳定排序」在完成排序后，相等素在数组中的相对位置 可能被改变 。例如：选择排序、快速排序、堆排序。

就地性：⁍

根据排序过程中 是否使用额外内存（辅助数组），排序算法可分为「原地排序」和「异地排序」两类。一般地，由于不使用外部内存，原地排序相比非原地排序的执行效率更高。

• 「原地排序」不使用额外辅助数组，例如：冒泡排序、插入排序、选择排序、快速排序、堆排序。

「非原地排序」使用额外辅助数组，例如：归并排序、基数排序、桶排序。

自适应性：⁍

根据算法 时间复杂度 是否 受待排序数组的元素分布影响 ，排序算法可分为「自适应排序」和「非自适应排序」两类。

• 「自适应排序」的时间复杂度受元素分布影响；例如：冒泡排序、插入排序、快速排序、桶排序。
• 「非自适应排序」的时间复杂度恒定；例如：选择排序、归并排序、堆排序、基数排序。

比较类：⁍

比较类排序基于元素之间的 比较算子（小于、相等、大于）来决定元素的相对顺序；相对的，非比较排序则不基于比较算子实现。

• 「比较类排序」基于元素之间的比较完成排序，例如：冒泡排序、插入排序、选择排序、快速排序、归并排序、堆排序。
• 「非比较类排序」不基于元素之间的比较完成排序，例如：基数排序、桶排序。

时空复杂度⁍

总体上看，排序算法追求时间与空间复杂度最低。而即使某些排序算法的时间复杂度相等，但实际性能还受 输入列表性质、元素数量、元素分布等 等因素影响。

设输入列表元素数量为$N$，常见排序算法的「时间复杂度」和「空间复杂度」如下图所示。

对于上表，需要特别注意：

• 「基数排序」适用于正整数、字符串、特定格式的浮点数排序，$k$ 为最大数字的位数；「桶排序」中 $k$ 为桶的数量。
• 普通「冒泡排序」的最佳时间复杂度为 $O(N^2)$，通过增加标志位实现 提前返回 ，可以将最佳时间复杂度降低至 $O(N)$。
• 在输入列表完全倒序下，普通「快速排序」的空间复杂度劣化至 $O(N)$，通过代码优化 Tail Call Optimization 保持算法递归较短子数组，可以将最差递归深度降低至 $\log N$。
• 普通「快速排序」总以最左或最右元素为基准数，因此在输入列表有序或倒序下，时间复杂度劣化至 $O(N^2)$；通过 随机选择基准数 ，可极大减少此类最差情况发生，尽可能地保持 $O(N \log N)$的时间复杂度。
• 若输入列表是数组，则归并排序的空间复杂度为 $O(N)$ ；而若排序 链表 ，则「归并排序」不需要借助额外辅助空间，空间复杂度可以降低至 $O(1)$ 。

冒泡排序⁍

• 内循环： 使用相邻双指针 j , j + 1 从左至右遍历，依次比较相邻元素大小，若左元素大于右元素则将它们交换；遍历完成时，最大元素会被交换至数组最右边 。
• 外循环： 不断重复「内循环」，每轮将当前最大元素交换至 剩余未排序数组最右边 ，直至所有元素都被交换至正确位置时结束。

// 冒泡排序
public void bubbleSort(int[] nums) {
    for (int i = 0; i < nums.length - 1; i++) {
        for (int j = 0; j < nums.length - i - 1; j++) {
            if (nums[j] > nums[j + 1]) {
                Common common = new Common();
                common.swap(j, j + 1, nums);
            }

        }
    }
}

复杂度分析：⁍

• 时间复杂度 $O(N^2)$ ： 其中 $N$ 为输入数组的元素数量；「外循环」共 $N - 1$ 轮，使用 $O(N)$ 时间；每轮「内循环」分别遍历 $N - 1$ , $N - 2$ , $\cdots$ , $2$ , $1$ 次，平均 $\frac{N}{2}$ 次，使用 $O(\frac{N}{2}) = O(N)$ 时间；因此，总体时间复杂度为 $O(N^2)$ 。

• 空间复杂度 $O(1)$ ： 只需原地交换元素，使用常数大小的额外空间。

算法特性：⁍

• 时间复杂度为 $O(N^2)$ ，因为其是通过不断 交换元素 实现排序（交换 2 个元素需要 3 次赋值操作），因此速度较慢；

• 原地： 指针变量仅使用常数大小额外空间，空间复杂度为 $O(1)$ ；

• 稳定： 元素值相同时不交换，因此不会改变相同元素的相对位置；

• 自适应： 通过增加一个标志位 flag ，若某轮内循环未执行任何交换操作时，说明已经完成排序，因此直接返回。此优化使冒泡排序的最优时间复杂度达到 $O(N)$（当输入数组已排序时）；

快速排序⁍

快速排序算法有两个核心点，分别为 哨兵划分 和 递归 。

• 哨兵划分： 以数组某个元素（一般选取首元素）为 基准数 ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

  • 流程： 取基准；将基准后面的元素进行划分——左边的是小于基准的元素，右边的是大于基准的元素；将基准交换至临界处；完毕。

• 递归： 对 左子数组 和 右子数组 分别递归执行 哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

  如下图所示，为示例数组 [2,4,1,0,3,5] 的快速排序流程。观察发现，快速排序和 二分法 的原理类似，都是以 $\log$ 时间复杂度实现搜索区间缩小。

  {:width=550}

int partition(int[] nums, int l, int r){
    // 基准nums[l]
    int i = l;
    int j = r;
    while(i < j){
        // 找从右往左第一个<基准的数
        while(i < j && nums[j] >= nums[l]){
            j--;
        }
        // 找从左往右第一个>基准的数
        while(i < j && nums[i] <= nums[l]){
            i++;
        }
        // 交换两个数
        Common common = new Common();
        common.swap(i, j, nums);

    }
    // 将基准交换到中间临界处
    Common common = new Common();
    common.swap(i, l, nums);

    return i;
}

public void quickSort(int[] nums, int l, int r){
    if (l >= r) return;
    int t = partition(nums, l, r);
    quickSort(nums, l, t-1);
    quickSort(nums, t+1, r);
}

public void quickSort(int[] nums){
    quickSort(nums, 0, nums.length - 1);
}

复杂度分析⁍

• 时间复杂度：

  • 最佳 $\Omega(N \log N )$ ： 最佳情况下， 每轮哨兵划分操作将数组划分为等长度的两个子数组；哨兵划分操作为线性时间复杂度 $O(N)$ ；递归轮数共 $O(\log N)$ 。

  • 平均 $\Theta(N \log N)$ ： 对于随机输入数组，哨兵划分操作的递归轮数也为 $O(\log N)$ 。

  • 最差 $O(N^2)$ ： 对于某些特殊输入数组，每轮哨兵划分操作都将长度为 $N$ 的数组划分为长度为 $1$ 和 $N - 1$ 的两个子数组，此时递归轮数达到 $N$ 。

    通过 「随机选择基准数」优化，可尽可能避免出现最差情况。

    每轮在子数组中随机选择一个元素作为基准数，这样就可以极大概率避免以上劣化情况。

    值得注意的是，由于仍然可能出现最差情况，因此快速排序的最差时间复杂度仍为$O(N^2)$。

    int partition(int[] nums, int l, int r) {
        // 在闭区间 [l, r] 随机选取任意索引，并与 nums[l] 交换
        int ra = (int)(l + Math.random() * (r - l + 1));
        swap(nums, l, ra);
        // 以 nums[l] 作为基准数，下同
    }

• 空间复杂度 $O(N)$ ： 快速排序的递归深度最好与平均皆为 $\log N$ ；输入数组完全倒序下，达到最差递归深度 $N$ 。

  通过「Tail Call」优化，可将最差空间复杂度降低至 $O(\log N)$ 。

  每轮递归时，仅对 较短的子数组 执行哨兵划分 partition() ，就可将最差的递归深度控制在 $O(\log N)$ （每轮递归的子数组长度都 $\leq$ 当前数组长度 $/ 2$ ），即实现最差空间复杂度 $O(\log N)$ 。

  void quickSort(int[] nums, int l, int r) {
      // 子数组长度为 1 时终止递归
      while (l < r) {
          // 哨兵划分操作
          int i = partition(nums, l, r);
          // 仅递归至较短子数组，控制递归深度
          if (i - l < r - i) {
              quickSort(nums, l, i - 1);
              l = i + 1;
          } else {
              quickSort(nums, i + 1, r);
              r = i - 1;
          }
      }
  }

算法特性⁍

• 虽然平均时间复杂度与「归并排序」和「堆排序」一致，但在实际使用中快速排序 效率更高 ，这是因为：

  • 最差情况稀疏性： 虽然快速排序的最差时间复杂度为 $O(N^2)$ ，差于归并排序和堆排序，但统计意义上看，这种情况出现的机率很低。大部分情况下，快速排序以 $O(N \log N)$ 复杂度运行。

  • 缓存使用效率高： 哨兵划分操作时，将整个子数组加载入缓存中，访问元素效率很高；堆排序需要跳跃式访问元素，因此不具有此特性。

  • 常数系数低： 在提及的三种算法中，快速排序的 比较、赋值、交换 三种操作的综合耗时最低（类似于插入排序快于冒泡排序的原理）。

• 原地： 不用借助辅助数组的额外空间，递归仅使用 $O(\log N)$ 大小的栈帧空间。

• 非稳定： 哨兵划分操作可能改变相等元素的相对顺序。

• 自适应： 对于极少输入数据，每轮哨兵划分操作都将长度为 $N$ 的数组划分为长度 $1$ 和 $N - 1$ 两个子数组，此时时间复杂度劣化至 $O(N^2)$ 。

归并排序⁍

归并排序体现了 “分而治之” 的算法思想，具体为：

• 「分」： 不断将数组从 中点位置 划分开，将原数组的排序问题转化为子数组的排序问题；

• 「治」： 划分到子数组长度为 1 时，开始向上合并，不断将 左右两个较短排序数组 合并为 一个较长排序数组，直至合并至原数组时完成排序；

如下图所示，为数组 [7,3,2,6,0,1,5,4] 的归并排序过程。

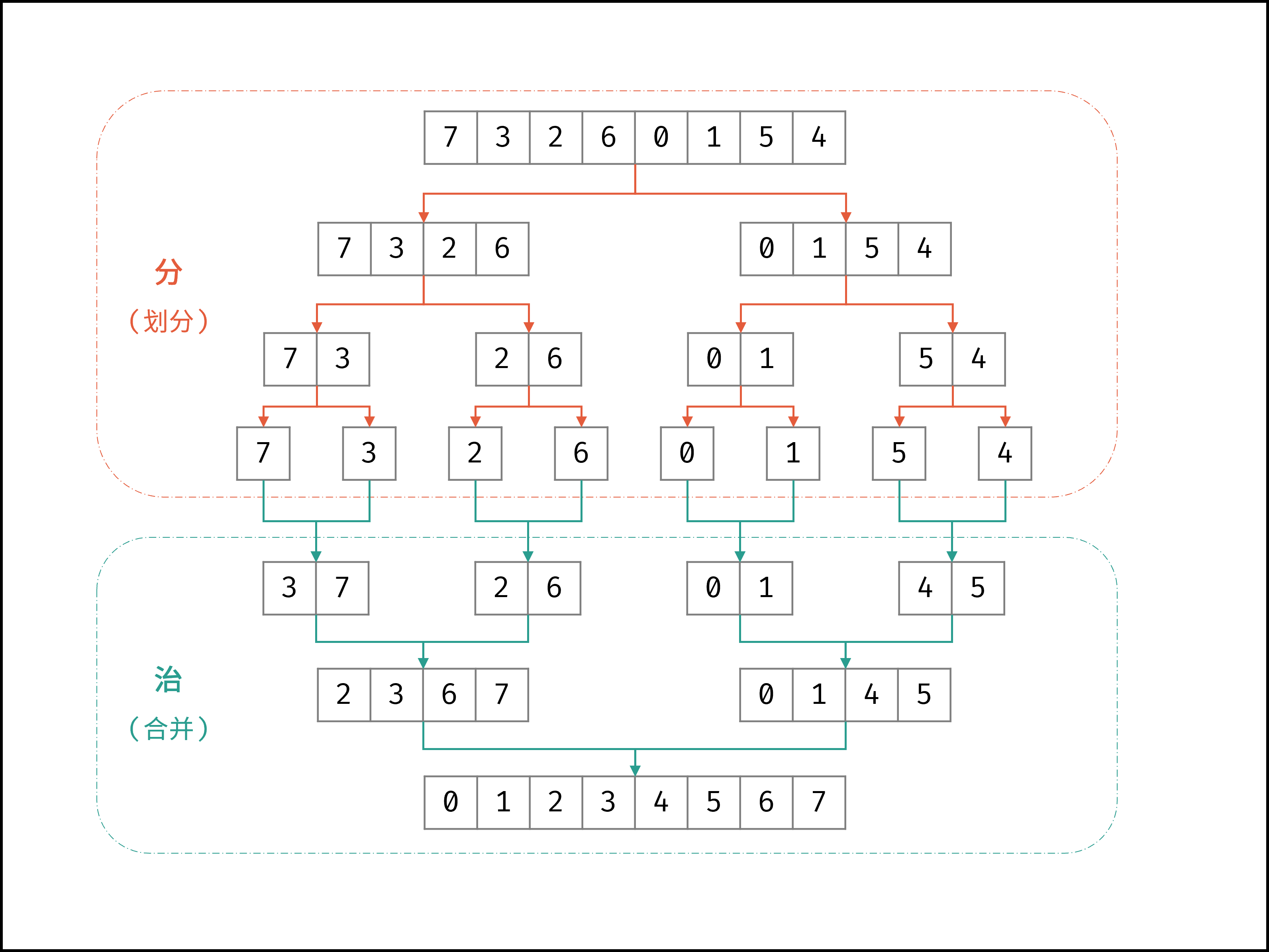{:width=500}

算法流程：⁍

1. 递归划分：

   1. 计算数组中点 $m$ ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r) ；

   2. 当 $l \geq r$ 时，代表子数组长度为 1 或 0 ，此时 终止划分 ，开始合并；

2. 合并子数组：

   1. 暂存数组 $nums$ 闭区间 $[l, r]$ 内的元素至辅助数组 $tmp$ ；

   2. 循环合并： 设置双指针 $i$ , $j$ 分别指向 $tmp$ 的左 / 右子数组的首元素；

      注意： $nums$ 子数组的左边界、中点、右边界分别为 $l$ , $m$ , $r$ ，而辅助数组 $tmp$ 中的对应索引为 $0$ , $m - l$ , $r - l$ ；

      • 当 $i == m - l + 1$ 时： 代表左子数组已合并完，因此添加右子数组元素 $tmp[j]$ ，并执行 $j = j + 1$ ；
      • 否则，当 $j == r - l + 1$ 时： 代表右子数组已合并完，因此添加左子数组元素 $tmp[i]$ ，并执行 $i = i + 1$ ；
      • 否则，当 $tmp[i] \leq tmp[j]$ 时： 添加左子数组元素 $tmp[i]$ ，并执行 $i = i + 1$ ；
      • 否则（即当 $tmp[i] > tmp[j]$ 时）： 添加右子数组元素 $tmp[j]$ ，并执行 $j = j + 1$ ；

public void mergeSort(int[] nums, int l, int r){
    if (l >= r) return;
    // 递归划分
    int m = (r + l) / 2;
    mergeSort(nums,l,m);
    mergeSort(nums,m+1,r);
    // 合并
    // 暂存需要合并的区间的元素
    int[] tmp = new int[r - l + 1];
    for (int k = l; k <= r; k++) {
        tmp[k-l] = nums[k];
    }
    // 设置双指针 i , j 分别指向 tmp 的左 / 右子数组的首元素
    int i = 0, j = m - l + 1;
    for (int k = l; k <= r; k++) {
        if (i == m - l + 1){
            nums[k] = tmp[j++];
        }else if (j == r - l + 1){
            nums[k] = tmp[i++];
        }else if (tmp[i] <= tmp[j]){
            nums[k] = tmp[i++];
        }else{
            nums[k] = tmp[j++];
        }
    }
}

public void mergeSort(int[] nums){
    mergeSort(nums, 0, nums.length-1);
}

复杂度分析⁍

• 时间复杂度： 最佳 $\Omega(N \log N )$ ，平均 $\Theta(N \log N)$ ，最差 $O(N \log N)$ 。

• 空间复杂度 $O(N)$ ： 合并过程中需要借助辅助数组 $tmp$ ，使用 $O(N)$ 大小的额外空间；划分的递归深度为 $\log N$ ，使用 $O(\log N)$ 大小的栈帧空间。

• 若输入数据是 链表 ，则归并排序的空间复杂度可被优化至 $O(1)$ ，这是因为：

  • 通过应用「双指针法」，可在 $O(1)$ 空间下完成两个排序链表的合并，省去辅助数组 $tmp$ 使用的额外空间；

  • 通过使用「迭代」代替「递归划分」，可省去递归使用的栈帧空间；

    详情请参考：148. 排序链表

算法特性⁍

• 非原地： 辅助数组 $tmp$ 需要使用额外空间。

• 稳定： 归并排序不改变相等元素的相对顺序。

• 非自适应： 对于任意输入数据，归并排序的时间复杂度皆相同。