Leetcode-贪心算法

基础知识⁍

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

什么时候用贪心 ：如何验证可不可以用贪心算法————举反例

贪心一般解题步骤⁍

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

406. 根据身高重建队列 ⁍

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面正好有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

思路：

先把people按身高hi排序

1	`[[7,0],[7,1],[6,1],[5,0],[5,2],[4,4]]`

从前到后，对于每个person，把它往前挪到第ki个位置 --> 直接用ArrayList实现

class Solution {

  public int[][] reconstructQueue(int[][] people) {
    // 身高从大到小排（身高相同k小的站前面）
    Arrays.sort(
      people,
      (a, b) -> {
        if (a[0] == b[0]) return a[1] - b[1];
        return b[0] - a[0];
      }
    );
    // 用Comparator实现
    // Arrays.sort(people, new Comparator<int[]>() {
    //     public int compare(int[] person1, int[] person2) {
    //         if (person1[0] != person2[0]) {
    //             return person2[0] - person1[0];
    //         } else {
    //             return person1[1] - person2[1];
    //         }
    //     }
    // });

    List<int[]> ans = new ArrayList<int[]>();

    for (int[] p : people) {
      ans.add(p[1], p);
    }

    return ans.toArray(new int[people.length][]);
  }
}

253. 会议室Ⅱ⁍

给你一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，返回所需会议室的最小数量。

示例 1：

输入：intervals = [[0,30],[5,10],[15,20]]
输出：2

示例 2：

输入：intervals = [[7,10],[2,4]]
输出：1

思路

先按每个interval的第1个元素排序

对所有会议，按照开始时间排升序；
用贪心算法，每来一个新的会议，遍历所有会议室，如果有空的会议室（该会议室的结束时间早于等于当前会议的开始时间），则作为当前最优的选择，更新该会议室的结束时间，并停止循环
如果一个可用的会议室都没有，则新增会议室，并更新该会议室的结束时间。

public int minMeetingRooms(int[][] intervals) {
    // 先考虑特殊情况
    if (intervals == null || intervals.length == 0)
        return 0;
    // 从定义排序按照进入时间排序
    Arrays.sort(intervals, (v1, v2) -> (v1[0] - v2[0]));
    // 定义一个优先队列
    PriorityQueue<Integer> heap = new PriorityQueue<>();
    // 一个计数器
    int meetingCount = 0;

    for (int[] meeting : intervals){
        //要是堆非空，当前会议的开始时间已经大于等于了最小的结束时间
        // 这里就是要把所有已经结束的会议淘汰出去
        while (!heap.isEmpty() && meeting[0] >= heap.peek()){
            heap.poll();
        }
        // 再把当前会议的结束时间加进去
        heap.add(meeting[1]); // 堆里有的就是进行的会议的数量
        // 谈话不断的看是不是最大的
        meetingCount = Math.max(meetingCount, heap.size());
    }
    return meetingCount;
}

⭐621. 任务调度器 ⁍

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 1：

输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
     在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。

示例 2：

输入：tasks = ["A","A","A","B","B","B"], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类

示例 3：

输入：tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出：16
解释：一种可能的解决方案是：
     A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

思路：

我们首先考虑所有任务种类中执行次数最多的那一种，记它为 $\texttt{A}$，的执行次数为 $\textit{maxExec}$。

使用一个宽为 $n+1$ 的矩阵可视化地展现执行 $\texttt{A}$ 的时间点。

任务以行优先的顺序执行，没有任务的格子对应 CPU 的待命状态。

fig1

冷却时间为 $n$，因此我们将所有的 $\texttt{A}$ 排布在矩阵的第一列，可以保证满足题目要求，同时这样时间也会最小

总时间： $$(n+1)(\textit{maxExec} - 1)+1$$

列数*行数，但是最后一行只需要一个A就行了，所以是

列数*（行数-1）+1

如果需要执行 $\textit{maxExec}$ 次（跟A次数相等）的任务的数量为 $\textit{maxCount}$，那么类似地可以得到对应的总时间为：

$$
(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$

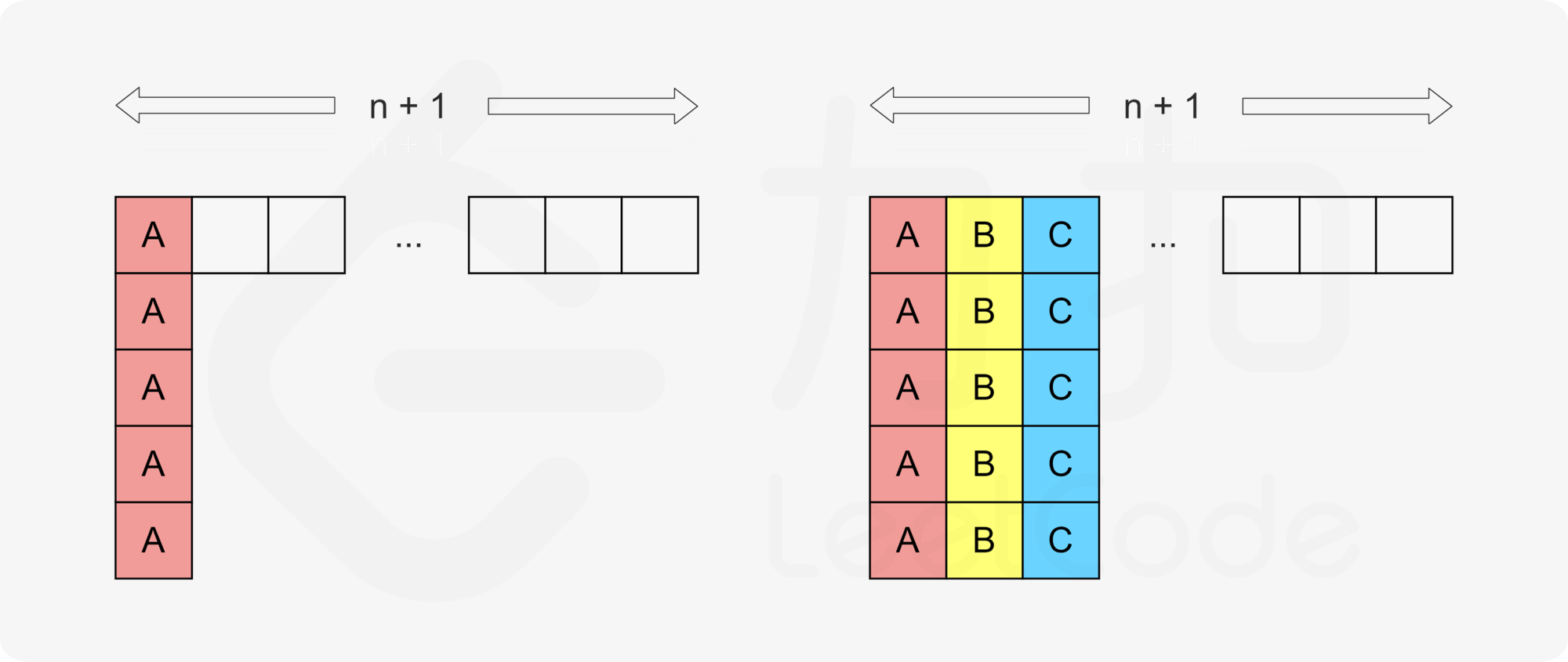
如果 $\textit{maxCount} > n+1$ （即不同的任务数量超过了冷却时间+1）?

问题放大就是填「超出」$n+1$ 列。如图

如果我们填「超出」了 $n+1$ 列，任意两个相邻任务的执行间隔肯定也会至少为 $n$

（可以把上图第二行的A挪到第1行的X，一次网上挪）

最后就是任务的总数 $|\textit{task}|$

fig2

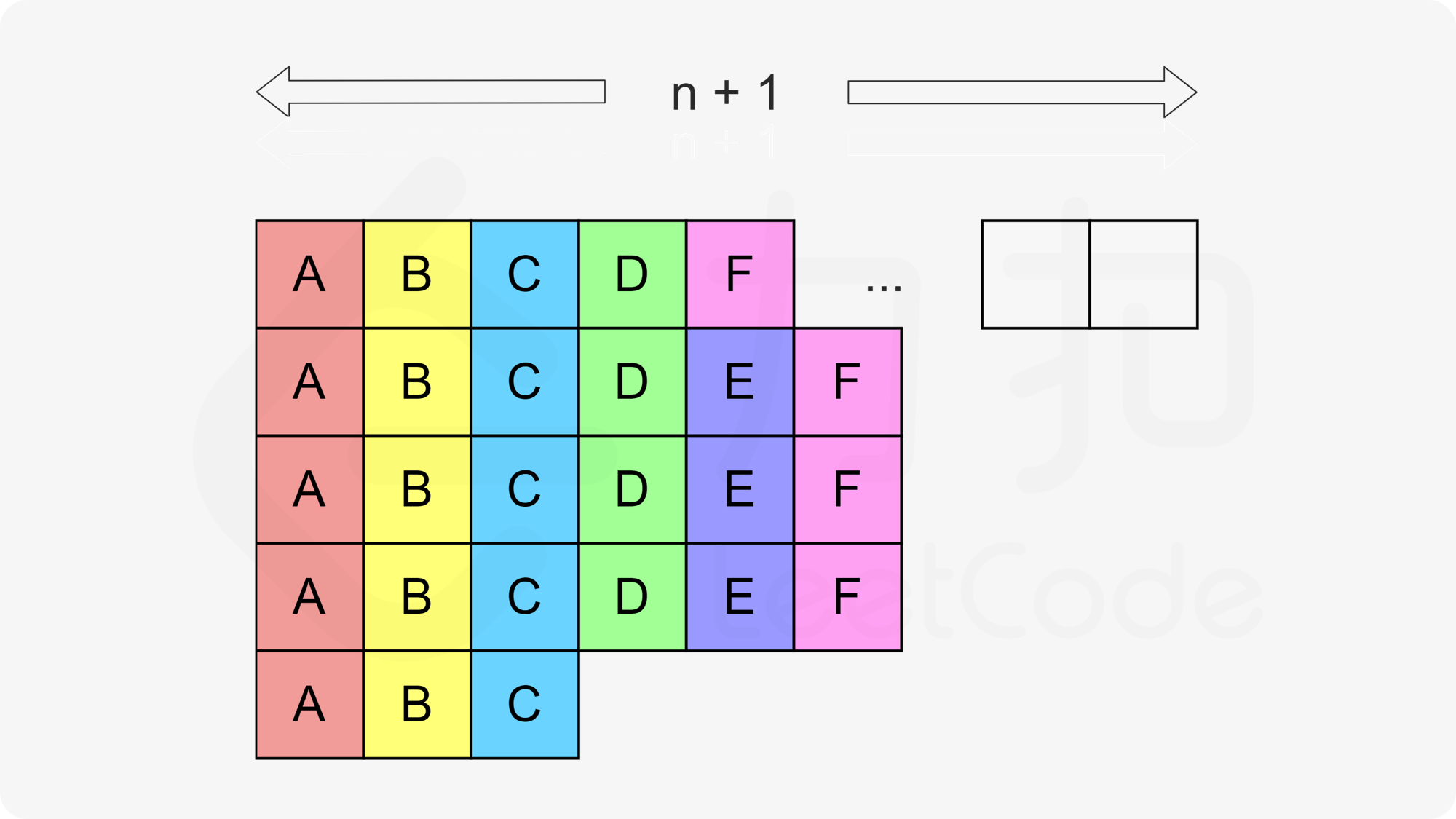
剩余任务的执行次数一定都小于 $\textit{maxExec}$，从 倒数第二行开始 ，按照 反向列优先的顺序（即先放入靠左侧的列，从下往上放） ，依次放入每一种任务，并且同一种任务需要连续地填入。

因为比$\textit{maxExec}$（即高度）小，所以同一行不可能出现两个同样的任务D/E/F，即满足题目要求，总时间还是不变的：
$$
(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$

综上：

如果我们没有填「超出」了 $n+1$ 列，那么图中存在 $0$ 个或多个位置没有放入任务，由于位置数量为 $(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}$，因此有：

$$
|\textit{task}| < (\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$
如果我们填「超出」了 $n+1$ 列，那么同理有：

$$
|\textit{task}| > (\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$

因此，在任意的情况下，需要的最少时间就是 $(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}$ 和 $|\textit{task}|$ 中的较大值。

class Solution {
    public int leastInterval(char[] tasks, int n) {
        Map<Character, Integer> freq = new HashMap<Character, Integer>();
        // 最多的执行次数
        int maxExec = 0;
        for (char ch : tasks) {
            int exec = freq.getOrDefault(ch, 0) + 1;
            freq.put(ch, exec);
            maxExec = Math.max(maxExec, exec);
        }

        // 具有最多执行次数的任务数量
        int maxCount = 0;
        Set<Map.Entry<Character, Integer>> entrySet = freq.entrySet();
        for (Map.Entry<Character, Integer> entry : entrySet) {
            int value = entry.getValue();
            if (value == maxExec) {
                ++maxCount;
            }
        }

        return Math.max((maxExec - 1) * (n + 1) + maxCount, tasks.length);
    }
}

复杂度分析

时间复杂度：$O(|\textit{task}| + |\Sigma|)$，其中 $|\Sigma|$ 是数组 $\textit{task}$ 中出现任务的种类，在本题中任务用大写字母表示，因此 $|\Sigma|$ 不会超过 $26$。
空间复杂度：$O(|\Sigma|)$。

用二维数组代替map：

class Solution {
    public int leastInterval(char[] tasks, int n) {
        int count[]=new int[26];
        for(int i=0;i<tasks.length;i++){count[tasks[i]-'A']++;}
        Arrays.sort(count);
        int j=25;
        while(j>=0&&count[j]==count[25]){j--;}//从j+1到25并列最多
        return Math.max(tasks.length,(n+1)*(count[25]-1)+25-j);
    }
}