基本知识[1][2]⁍

虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。

因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

回溯法问题总结⁍

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

组合无序，排序有序

回溯法模板⁍

回溯法解决的问题都可以抽象为树形结构，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

⭐ 回溯三步：⁍

  • 回溯函数模板返回值（一般是void）以及参数

    • 一般是先写逻辑，然后需要什么参数，就填什么参数。

      1
      void backtracking(参数)

  • 回溯函数终止条件

    一般来说搜到 叶子节点 了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

    所以回溯函数终止条件伪代码如下：

    1
    2
    3
    4
    if (终止条件) {
        存放结果;
        return;
    }

  • 回溯搜索的遍历过程

    回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

    回溯算法理论基础

    for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历

    1
    2
    3
    4
    5
    6
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }

    不能忘记回溯撤销

组合问题⁍

77. 组合⁍

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

思路

  • 叶子节点：每个组合的第k个数，即子组合长度为k
  • 每个节点就是往集合里加数
  • 横向遍历： 剪枝 [起始,剩下的数]（不剪枝就是<=n）
    • 关键：如何避免重复？——每次递归的时候取[]中下一个数
    • 起始：i=t，递归时变成i+1
    • 剩下的数：= n - 集合中还差的数的个数 +1 （保证还有足够的数可以被遍历）
      • 集合中还差的数的个数 = （k-comb.size()）

77.组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
  public List<List<Integer>> res = new ArrayList<List<Integer>>();
  public LinkedList<Integer> comb = new LinkedList<>();

  public List<List<Integer>> combine(int n, int k) {
    backtracking(n, k, 1);
    return res;
  }

  public void backtracking(int n, int k, int t) {
    if (comb.size() == k) {
      res.add(new ArrayList<>(comb));
      return;
    }
    for (int i = t; i <= n - (k - comb.size()) + 1; i++) {
      comb.add(i);
      backtracking(n, k, i + 1);
      comb.removeLast();
    }
  }
}

216. 组合总和 III⁍

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

思路： 参考上面的模板，一下就写对啦！

  • 终止条件：
    • size=k且sum=n，符合条件，res.add
    • size=k但sum!=n，结束
    • 按从小到大遍历的话，如果sum>n，结束
  • 横向遍历 [1,9]–》[t,9-(k-size)+1], t=i+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
  public List<List<Integer>> res = new ArrayList<>();
  public LinkedList<Integer> path = new LinkedList<>();
  public int sum = 0;

  public List<List<Integer>> combinationSum3(int k, int n) {
    sumComb3(k, n, 1);
    return res;
  }

  public void sumComb3(int k, int n, int startIndex) {
    int sz = path.size();
    if (sz == k && sum == n) {
      res.add(new ArrayList<>(path));
      return;
    }
    if (sum > n || (sz == k && sum != n)) {
      return;
    }

    for (int i = startIndex; i <= 9 - (k - sz) + 1; i++) {
      sum += i;
      path.add(i);
      sumComb3(k, n, i + 1);
      path.removeLast();
      sum -= i; // 别忘了回溯这一步！
    }
  }
}

⭐17. 电话号码的字母组合⁍

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

17.电话号码的字母组合

示例 1：

1
2
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

1
2
输入：digits = ""
输出：[]

示例 3：

1
2
输入：digits = "2"
输出：["a","b","c"]

思路：

首先要思考清楚题意，每个数字相当于一个字母的集合（用字符串数组表示出来）

每个集合里都要取一个数，构成最终的集合

因为是集合（答案可以按任意顺序返回），所以按顺序来就行

  • 每层迭代是每个数字内部的集合遍历
  • 每层递归是下一个“数字”代表的集合
  • 终止条件是没有数字了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
  public final String[] digitStr = {
    "",
    "",
    "abc", //2
    "def", //3
    "ghi", //4
    "jkl", //5
    "mno", //6
    "pqrs", //7
    "tuv", //8
    "wxyz", //9
  };

  public List<String> res = new ArrayList<>();

  public List<String> letterCombinations(String digits) {
    if (digits == null || digits.length() == 0) {
      return res;
    }
    // 每次迭代获取一个字符串，所以会设计大量的字符串拼接，所以这里选择更为高效的 StringBuilder
    StringBuilder temp = new StringBuilder();
    backtracking(digits, 0, temp);
    return res;
  }

  public void backtracking(String digits, int i, StringBuilder temp) {
    // i记录迭代到第i个digits

    if (i == digits.length()) {
      //   res.add(str);
      res.add(temp.toString());
      return;
    }
    // k记录遍历到当前digit里的第k位
    int digit = digits.charAt(i) - '0';
    for (int k = 0; k < digitStr[digit].length(); k++) {
      //   str += digitStr[digit].charAt(k);
      temp.append(digitStr[digit].charAt(k));
      backtracking(digits, i + 1, temp);
      //   str = str.substring(0, str.length() - 1);
      temp.deleteCharAt(temp.length() - 1);
    }
  }
}

关键问题和错误：

  1. 涉及字符串拼接，选用StringBuilder
    • 转换成String： .toString()
    • 添加：.append(ch)
    • 删除最后一个：deleteCharAt(temp.length() - 1);
  2. 字符串的第K个字母： .charAt(k)
  3. ⭐ digit的第k位，转换为数字：int digit = digits.charAt(i) - '0';

39. 组合总和⁍

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

思路： 先排序

这题在[数组](/augu1sto/0d8a87a8eab4/#39-组合总和)里写过，不赘述

  • 终止条件
    • sum==target，加进结果列表，返回
    • sum>target，再往后遍历也更大，直接返回
      • 虽然我也不是很懂，这个判断条件写进循环里，效率会高很多。。
  • 遍历，因为排序过了，每次从下一个值开始遍历 ❌
    • 可以重复，从当前值开始遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Integer>> res = new ArrayList<>();
    public LinkedList<Integer> path = new LinkedList<>();
    public int sum = 0;

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);//排序
        sumComb(candidates, target, 0);
        return res;
    }

    public void sumComb(int[] nums, int target, int startIndex) {
        
        if(sum==target){
            res.add(new ArrayList<>(path));
            return;
        }
        // if (sum>target) {
        //     return;
        // }
        for (int i = startIndex; i < nums.length&&(sum+nums[i]<=target); i++) {
            sum+=nums[i];
            path.add(nums[i]);
            sumComb(nums, target, i);
            sum-=nums[i];
            path.removeLast();
        }
    }
}

40. 组合总和 II⁍

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意： 解集不能包含重复的组合。

思路

和上一题差不多，遍历的时候从下一个数开始就行了

但是要去重，也就是说for循环的时候如果下一个数和当前数相等，跳过continue就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public List<List<Integer>> res = new ArrayList<>();
    public LinkedList<Integer> path = new LinkedList<>();
    public int sum = 0;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);//排序
        sumComb2(candidates, target, 0);
        return res;
    }

    public void sumComb2(int[] nums, int target, int startIndex) {
        
        if(sum==target){
            res.add(new ArrayList<>(path));
            return;
        }
        // if (sum>target) {
        //     return;
        // }
        for (int i = startIndex; i < nums.length&&(sum+nums[i]<=target); i++) {
            if (i>startIndex&&nums[i]==nums[i-1]) {//去重
                continue;
            }
            sum+=nums[i];
            path.add(nums[i]);
            sumComb2(nums, target, i+1);//这里！
            sum-=nums[i];
            path.removeLast();
        }
    }
}

切割问题⁍

从startIndex循环，确定长度

切割条件的判断，不满足条件就continue

131. 分割回文串⁍

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

1
2
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

思路

两个关键问题：

  1. 切割问题，有不同的切割方式
  2. 判断回文
  • 终止条件：
    • 遍历到结尾，加入合集
  • 逻辑：
    • 用startIndex表示切割线
    • 循环i表示切割长度
    • 如果是回文就记录到path中
  • 优化：记忆化搜索
    • 用f[i][j] = 0 表示未搜索，1 表示是回文串，-1 表示不是回文串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    List<List<String>> res = new ArrayList<>();
    LinkedList<String> path = new LinkedList<>();
    int[][] f;
    
    public List<List<String>> partition(String s) {
        f = new int[s.length()][s.length()];
        backtracking(s, 0);
        return res;
    }

    public void backtracking(String s, int startIndex) {
        if (startIndex>=s.length()) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            String st = s.substring(startIndex, i+1);//右边取不到，所以写i+1
            if (isPal(s,startIndex,i)==-1) {
                continue;
            }
            path.add(st);
            backtracking(s, i+1);
            path.removeLast();
        }
    }

    // 记忆化搜索中，f[i][j] = 0 表示未搜索，1 表示是回文串，-1 表示不是回文串
    public int isPal(String s, int i, int j) {
        if (f[i][j] != 0) {
            return f[i][j];
        }
        if (i >= j) {
            f[i][j] = 1;
        } else if (s.charAt(i) == s.charAt(j)) {
            f[i][j] = isPal(s, i + 1, j - 1);
        } else {
            f[i][j] = -1;
        }
        return f[i][j];
    }

}

93. 复原 IP 地址⁍

用以表示一个 IP 地址，返回所有可能的有效 IP 地址 (不能有前缀0)，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

1
2
输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

思路

  • 除了index，还要用cnt来记录是第几次切割，根据剩下的位数len-startIndex剪枝
    • 第1次前：4~12位
    • 第2次前：3~9位
    • 第3次前：2~6位
    • 第4次前：1~3位
    • 总结：(4-cnt+1) ~ 3*(4-cnt+1)位
  • 每次切割最多3位
  • 如果首字母==0，只能切1位
  • 有效：转换为十位数在0-255之间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public List<String> res = new ArrayList<>();
    public String[] arr = new String[4];
    public List<String> restoreIpAddresses(String s) {
        cutting(s, 0, 1);
        return res;
    }

    public void cutting(String s, int startIndex, int cnt) {
        if (startIndex==s.length()&&cnt==4+1) {
            res.add(String.join(".", arr));
            return;
        }
        if ((s.length()-startIndex<4-cnt+1)||(s.length()-startIndex>3*(4-cnt+1))) {
            return;
        }
        if(s.charAt(startIndex)=='0'){
            arr[cnt-1]="0";
            cutting(s, startIndex+1, cnt+1);
            //用cnt记录回溯，不用再做操作
            return;
        }
        //for循环注意最后的条件，不能超出字符串长度
        for (int i = startIndex; i < s.length()&&i < startIndex+3; i++) {
            String st = s.substring(startIndex, i+1);
            if (Integer.parseInt(st)<0||Integer.parseInt(st)>255) {
                continue;
            }

            arr[cnt-1]=st;
            cutting(s, i+1, cnt+1);
            //用cnt记录回溯，不用再做操作
            
        }
    }

}

数据结构选型

字符串数组长度固定+要用特定字符拼接：用String[]

注意细节！！

子集问题⁍

组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点

78. 子集⁍

遍历时记录所有节点(写在递归开头)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
  public List<List<Integer>> res = new ArrayList<>();
  public LinkedList<Integer> path = new LinkedList<>();

  public List<List<Integer>> subsets(int[] nums) {
    backtracking(nums, 0);
    return res;
  }

  public void backtracking(int[] nums, int startIndex) {
    res.add(new ArrayList<>(path));//记录
    if (startIndex == nums.length) {
      return;
    }
    for (int i = startIndex; i < nums.length; i++) {
      path.add(nums[i]);
      backtracking(nums, i + 1);
      path.removeLast();
    }
  }
}

90. 子集 II⁍

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

思路 先排序，循环遍历时跳过和上一个一样的数（参考组合）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
  public List<List<Integer>> res = new ArrayList<>();
  public LinkedList<Integer> path = new LinkedList<>();

  public List<List<Integer>> subsetsWithDup(int[] nums) {
    Arrays.sort(nums);
    backtracking(nums, 0);
    return res;
  }

  public void backtracking(int[] nums, int startIndex) {
    res.add(new ArrayList<>(path));
    if (startIndex == nums.length) {
      return;
    }
    for (int i = startIndex; i < nums.length; i++) {
      if (i > startIndex && nums[i] == nums[i - 1]) { //去重
        continue;
      }
      path.add(nums[i]);
      backtracking(nums, i + 1);
      path.removeLast();
    }
  }
}

491. 递增子序列⁍

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

思路： 套子集模板

  • 判断数字是否>=Path的最后一个数，如果不是，则continue；

  • 注意递增子序列中 至少有两个元素 。

  • 去重

    • -100 <= nums[i] <= 100
    • 用长度为200的数组记录数字有没有被访问过(每层！！写在递归里面，循环外面)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
  public List<List<Integer>> res = new ArrayList<>();
  public LinkedList<Integer> path = new LinkedList<>();

  public List<List<Integer>> findSubsequences(int[] nums) {
    backtracking(nums, 0);
    return res;
  }

  public void backtracking(int[] nums, int startIndex) {
    if (path.size() >= 2) {
      res.add(new ArrayList<>(path));
    }
    if (startIndex == nums.length) {
      return;
    }
    int[] visited = new int[201]; //记录数是否被访问过，访问过的(数+100)对应置1

    for (int i = startIndex; i < nums.length; i++) {
      if (
        !path.isEmpty() &&
        nums[i] < path.getLast() ||
        (visited[nums[i] + 100] == 1)
      ) {
        continue;
      }
      visited[nums[i] + 100] = 1;
      path.add(nums[i]);
      backtracking(nums, i + 1);
      path.removeLast();
    }
  }
}

排列问题⁍

46. 全排列⁍

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

思路

不需要startIndex，但是要去重，记录哪些元素用过了（记得回溯）

和上一题不同，这次直接申请nums长度的used数组就行了

used[i]表示num[i]是否出现过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
  public List<List<Integer>> res = new ArrayList<>();
  public LinkedList<Integer> path = new LinkedList<>();
  public boolean[] used;

  public List<List<Integer>> permute(int[] nums) {
    used = new boolean[nums.length];
    backtracking(nums);
    return res;
  }

  public void backtracking(int[] nums) {
    if (path.size() == nums.length) {
      res.add(new ArrayList<>(path));
      return;
    }

    for (int i = 0; i < nums.length; i++) {
      if (used[i]) {
        continue;
      }

      used[i] = true;
      path.add(nums[i]);
      backtracking(nums);
      path.removeLast();
      used[i] = false;
    }
  }
}

⭐ 47. 全排列 II⁍

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

思路

先排序，遍历时比较节点的值是否与上一个相同（line22），记得查看是否被访问过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
  public List<List<Integer>> res = new ArrayList<>();
  public LinkedList<Integer> path = new LinkedList<>();
  public boolean[] used;

  public List<List<Integer>> permuteUnique(int[] nums) {
    used = new boolean[nums.length];
    Arrays.sort(nums);
    backtracking(nums);
    return res;
  }

      public void backtracking(int[] nums) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
            // used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
            // 如果同⼀树层nums[i - 1]使⽤过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            //如果同⼀树⽀nums[i]使⽤过
            if (used[i] == true) {
                continue;
            }
            used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用
            path.add(nums[i]);
            backTrack(nums, used);
            path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
            used[i] = false;//回溯
            }
        }
    }
}

如果改成 used[i - 1] == true， 也是正确的!，去重代码如下：

1
2
3
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
    continue;
}

如果要对树层中前一位去重，就用used[i - 1] == false，如果要对树枝前一位去重用used[i - 1] == true。

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

⭐332. 重新安排行程⁍

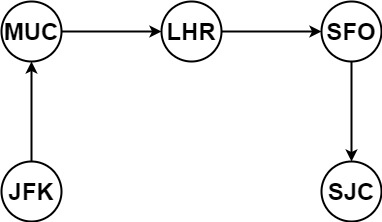
给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

  • 例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

示例 1：

img

1
2
输入：tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]
输出：["JFK","MUC","LHR","SFO","SJC"]

思路

建立{起点：{终点}}的映射集合：用Map

其中{终点}要以字典序排序，所以选用有自然优先级的容器TreeMap（回溯）/PriorityQueue（官方题解dfs）

下面是回溯法的步骤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
  private Deque<String> res;
  private Map<String, Map<String, Integer>> map;

  public List<String> findItinerary(List<List<String>> tickets) {
    map = new HashMap<String, Map<String, Integer>>();
    res = new LinkedList<>();
    for (List<String> t : tickets) {
      Map<String, Integer> temp;
      if (map.containsKey(t.get(0))) {
        temp = map.get(t.get(0));
        temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
      } else {
        temp = new TreeMap<>(); //升序Map
        temp.put(t.get(1), 1);
      }
      map.put(t.get(0), temp);
    }
    res.add("JFK");
    backTracking(tickets.size());
    return new ArrayList<>(res);
  }

  private boolean backTracking(int ticketNum) {
    if (res.size() == ticketNum + 1) {
      return true;
    }
    String last = res.getLast();
    if (map.containsKey(last)) { //防止出现null
      for (Map.Entry<String, Integer> target : map.get(last).entrySet()) {
        int count = target.getValue();
        if (count > 0) {
          res.add(target.getKey());
          target.setValue(count - 1);
          if (backTracking(ticketNum)) return true;
          res.removeLast();
          target.setValue(count);
        }
      }
    }
    return false;
  }
}

方法二： DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    Map<String, PriorityQueue<String>> map = new HashMap<String, PriorityQueue<String>>();
    List<String> itinerary = new LinkedList<String>();

    public List<String> findItinerary(List<List<String>> tickets) {
        for (List<String> ticket : tickets) {
            String src = ticket.get(0), dst = ticket.get(1);
            if (!map.containsKey(src)) {
                map.put(src, new PriorityQueue<String>());
            }
            map.get(src).offer(dst);
        }
        
        dfs("JFK");
        Collections.reverse(itinerary);
        return itinerary;
    }

    public void dfs(String curr) {
        while (map.containsKey(curr) && map.get(curr).size() > 0) {
            String tmp = map.get(curr).poll();
            dfs(tmp);
        }
        itinerary.add(curr);
    }
}

//作者：LeetCode-Solution
//链接：https://leetcode-cn.com/problems/reconstruct-itinerary/solution/zhong-xin-an-pai-xing-cheng-by-leetcode-solution/

⭐51. N 皇后⁍

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

img

1
2
3
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

1
2
输入：n = 1
输出：[["Q"]]

思路：

皇后们的约束条件：

  1. 不能同行
  2. 不能同列
  3. 不能同斜线

用4个数组记录该行、列、左斜/右斜有没有被访问过

因为在单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，所以不用去重了。

对于cb[row][col]

  • used_c[col]==1，说明被访问过
  • 左斜线可以用 used_l[row+col]==1，表示访问过
  • 右斜线可以用 used_r[n-1-row+col]==1，表示访问过

image-20220224102045206

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    List<List<String>> res = new ArrayList<>();
    String[] path;//最后用Arrays.asList转换
    int[] used_c;
    int[] used_l;
    int[] used_r;
    public List<List<String>> solveNQueens(int n) {
        path = new String[n];
        used_c = new int[n];//是否用过当前列
        used_l = new int[2*n-1];//是否用过左斜线
        used_r = new int[2*n-1];//是否用过右斜线
        helper(n, 0);
        return res;
    }

    public void helper(int n, int row) {
        if (row==n) {
            res.add(new ArrayList(Arrays.asList(path)));//ATTENTION!
            return;
        }
        char[] st = new char[n];
        Arrays.fill(st, '.');//初始化填充.
        for (int col = 0; col < n; col++) {
            if (used_c[col]==1||used_l[row+col]==1||used_r[n-1-row+col]==1) {
                continue;
            }
            //set
            st[col]='Q';
            used_c[col]=1;
            used_l[row+col]=1;
            used_r[n-1-row+col]=1;
            path[row]=new String(st);//转换成String填入path
            helper(n, row+1); //下一行
            //reset
            st[col]='.';
            used_c[col]=0;
            used_l[row+col]=0;
            used_r[n-1-row+col]=0; 

        }
        
    }

}

注意：

使用的类型以及类型转化

引用类型要new一个再传参

String没有办法随便更改某一位的值，故这里用char[]再进行转换

说不定有其他更方便的数据结构

37. 解数独⁍

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

  • 题目数据 保证 输入数独仅有一个解

思路

对每一个数看三个地方有没有重复解：

  • 行 new row[9]
  • 列 new col[9]
  • 块 new block[9]

image-20220224163800447

用行r和列c来表示第b块 b=3*(r/3)+c/3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Solution {
    int[][] row = new int[9][9];
    int[][] col = new int[9][9];
    int[][] block = new int[9][9];
    public void solveSudoku(char[][] board) {

        //记录已有的数
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board.length; j++) {
                if (board[i][j]!='.') {
                    int num = board[i][j]-'0';
                    row[num-1][i] = 1;
                    col[num-1][j] = 1;
                    block[num-1][3*(i/3)+j/3] = 1;
                }
            }
        }

        solve(board);
    }

    public boolean solve(char[][] board) {

        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j]!='.') {
                    continue;
                }
                for (int num = 1; num <= 9; num++) {
                    if (!checkValid(board, i, j, num)) {
                        continue;
                    }

                    board[i][j]=(char)(num+'0');
                    row[num-1][i] = 1;
                    col[num-1][j] = 1;
                    block[num-1][3*(i/3)+j/3] = 1;
                    if (solve(board)) {//如果找到合适一组立刻返回
                        return true;
                    }

                    board[i][j]='.';
                    row[num-1][i] = 0;
                    col[num-1][j] = 0;
                    block[num-1][3*(i/3)+j/3] = 0;                    

                }
                return false;//找不到，返回错误
            }
        }
        //遍历完没有返回false，说明找到了合适棋盘位置了
        return true;
    }

    public boolean checkValid(char[][] board, int i, int j, int num) {
        if (row[num-1][i]==1||col[num-1][j]==1||block[num-1][3*(i/3)+j/3]==1) {
            return false;
        }
        return true;
    }

}

我的老天爷！！！把除号和模号搞错了！！纠结好久。。救命

runtime beats 53.4 %

或许用其他方法更快？（位运算，见官方题解）

  1. 代码随想录 (programmercarl.com) ↩︎

  2. 带你学透回溯算法（理论篇）| 回溯法精讲！_哔哩哔哩_bilibili ↩︎