leetbook《数组和字符串》笔记
leetcode相关题思路整理（待整理）

豆知识⁍

1. 看到O(logN)就要去联想二分法⁍

704. 二分法解题思路[1]：

  • 在[left,right]闭区间内找条件对应： left<=right left=mid+1 right=mid-1

    • （左闭右开，则left<right left=mid+1 right=mid）

  • 防止溢出： mid=left+((right-left)>>1))

  • 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算

1
2
3
if (target < nums[0] || target > nums[nums.length - 1]) {
   return -1;
  }

相关题

34. 在排序数组中查找元素的第一个和最后一个位置

35. 搜索插入位置

69.x 的平方根

367.有效的完全平方数

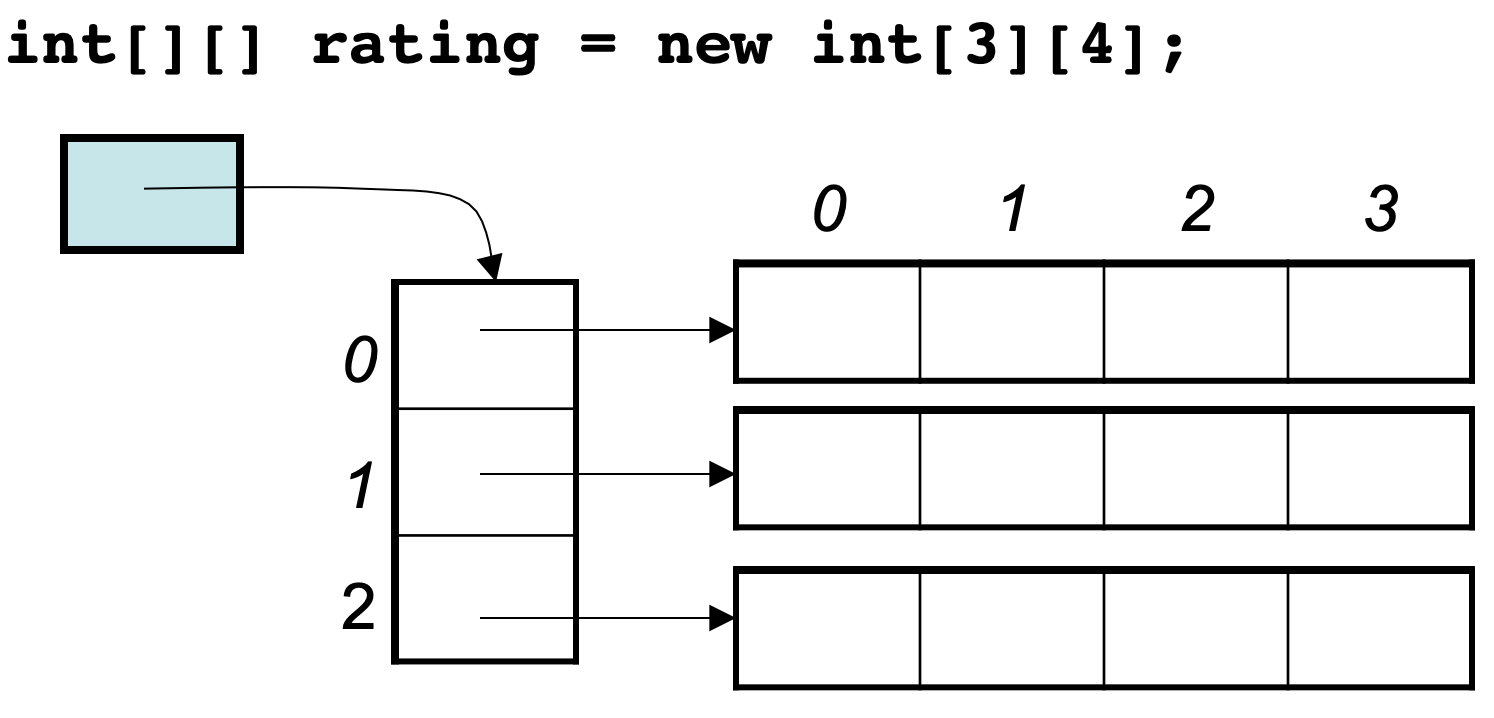
2. Java与C++在二维数组上寻址的区别[2]⁍

C++中二维数组在地址空间上是连续的。

像Java是没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。所以看不到每个元素的地址情况。

所以Java的二维数组可能是如下排列的方式：

算法通关数组3

3. 双指针法[3]⁍

27.移除元素-双指针法

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

  • 暴力解法时间复杂度：$O(n^2)$
  • 双指针时间复杂度：$O(n)$

双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组和链表操作的面试题，都使用双指针法。

相关题目：

  • 26.删除排序数组中的重复项
  • 283.移动零
  • 844.比较含退格的字符串
  • 977.有序数组的平方

另一种双指针是一头一尾

4. 滑动窗口[3:1]⁍

本题介绍了数组操作中的另一个重要思想：滑动窗口。

  • 暴力解法时间复杂度：$O(n^2)$
  • 滑动窗口时间复杂度：$O(n)$

本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。

如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。

相关题目：

5. 模拟行为[3:2]⁍

模拟过程，定义动作

在这道题目中，我们再一次介绍到了循环不变量原则，其实这也是写程序中的重要原则。

循环不变量：按固定的规则遍历，比如 左闭右闭，左闭右开 之类的，二分法里有。

相关题目：

  • 54.螺旋矩阵
  • 剑指Offer 29.顺时针打印矩阵

寻找数组的中心索引⁍

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

ag: 数组；前缀和

思路：

  1. 先求得数组中所有元素之和sum；
  2. 遍历数组，取当前下标左边的元素之和left_sum，同时sum减去已遍历元素，比较二者是否相等，相等则返回当前下标；
  3. 遍历结束，代表没有中心索引，返回-1；

作者：xiaoyi
链接：https://leetcode-cn.com/leetbook/read/array-and-string/yf47s/?discussion=D6slGT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int pivotIndex(int[] nums) {
        int sum = 0;
        for(int i=0;i<nums.length;i++){
            sum += nums[i];
        }
        int left_sum = 0;
        for(int i=0;i<nums.length;i++){
            sum -= nums[i];
            if(left_sum == sum){
                return i;
            }
            left_sum += nums[i];
        }
        return -1;
    }
}

对角线遍历⁍

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

示例 1：

img

输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public static int[] findDiagonalOrder(int[][] matrix) {
        if (matrix.length == 0) {
            return new int[0];
        }
        int m = matrix.length;
        int n = matrix[0].length;
        //存放数组
        int[] ans = new int[m * n];
        //对角线方向次数
        int count = n + m - 1;
        //定义初始化 行标记，列标记，存放数组索引
        int row = 0, col = 0, Index = 0;
        //开始对角线循环
        for (int i = 0; i < count; i++) {
            //判断对角线方向（因题目初始从右上（即i=0）开始）：偶数右上，奇数左下
            if (i % 2 == 0) {
                //右上操作
                while (row >= 0 && col < n) {
                    //将矩阵数存入存放数组
                    ans[Index] = matrix[row][col];
                    //索引后移
                    Index++;
                    //右上规律：行减一，列加一
                    row--;
                    col++;
                }
                //判断是否为越界情况：不越界正常行加一，越界行加二，列减一；
                //（此处不理解的拿张草稿纸将循环中row和col的值遍历写一下对照矩阵图就明白了）
                if (col < n) {
                    row++;
                }
                else {
                    row += 2;
                    col--;
                }
            }
            //左下操作：按规律与右上相反即可
            else {
                while (row < m && col >= 0) {
                    ans[Index] = matrix[row][col];
                    Index++;
                    row++;
                    col--;
                }
                if (row < m) {
                    col++;

                } else {
                    row--;
                    col += 2;
                }
            }
        }
        // 返回存放数组
        return ans;
    }

作者：bsyc
链接：https://leetcode-cn.com/leetbook/read/array-and-string/cuxq3/?discussion=iKJs16
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

31. 下一个排列⁍

实现获取 下一个排列 的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列（即，组合出下一个更大的整数）。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须 原地 修改，只允许使用额外常数空间。

思路：

思考不存在更大排列的情况（即排列已经是最大了的情况），此时，数组肯定是倒序的。

所以我们只需要从后往前找到第一个不是倒序的数，再进行调整。

fig1

  1. 找a[i-1]，从后往前数，它是第一个满足非降序即a[i-1]<a[i]的
  2. 找a[j]，从后往前数，它是第一个大于a[i-1]的
  3. 交换a[i-1]和a[j]，并对a[i-1]后面的数升序排列（反转）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {

  public void nextPermutation(int[] nums) {
    int i = nums.length - 1;
    while (i > 0 && nums[i - 1] >= nums[i]) {
      i--;
    }
    if (i > 0) {
      int j = nums.length - 1;

      while (nums[j] <= nums[i - 1]) {
        j--; //&&j>=0?
      }
      swap(nums, i - 1, j);
    }
    reverse(nums, i, nums.length - 1);
  }

  public void reverse(int[] num, int i, int j) {
    //反转num[i~j]之间的数组排列
    while (i < j) {
      swap(num, i, j);
      i++;
      j--;
    }
  }

  public void swap(int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
  }
}

34. 在排序数组中查找元素的第一个和最后一个位置⁍

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

思路：

传统解法，需要设置标志位看从左侧找还是右侧找（官方题解）

解法二 将问题转化为 找 target-1和target的最右侧值a和b，最后的区间是（a+1,b）。需要思考的是，此处的target-1代表的是仅次于target大小的数（也有可能是target-2之类的），故binarySearch寻找的是第一个大于target的数，接收完返回值只需-1即可

注意细节（转化后的问题可以理解为35. 搜索插入位置）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {

  public int[] searchRange(int[] nums, int target) {
    int a = -1;
    int b = -1;

    a = binaryFind(nums, target - 1); //target的左界=第一个大于target-1的数
    b = binaryFind(nums, target) - 1; //target的右界=第一个大于target的数-1
    if (a <= b && nums[b] == target) return new int[] { a, b };
    // a<b的情况，low>high（空集）时，res直接返回
    return new int[] { -1, -1 };
  }

  public int binaryFind(int[] nums, int target) {
    //返回第一个大于target的数的下标
    int low = 0;
    int high = nums.length - 1;
    int res = nums.length; //考虑到空集的情况，结果还要-1，故这里取nums.length

    while (low <= high) {
      int mid = (high + low) / 2;
      if (nums[mid] > target) {
        high = mid - 1; //不断向target逼近，若此时刚好跳出，则mid比target坐标刚好大1
        res = mid;
      } else {
        low = mid + 1;
      }
    }
    return res;
  }
}

39. 组合总和⁍

见回溯，下同

40. 组合总和 II⁍

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

**注意：**解集不能包含重复的组合。

和39题的区别：candidates中的数有重复的（但不能有重复的组合）；candidates 中的每个数字在每个组合中只能使用一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {

  public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    // int len = candidates.length;
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    //排序
    Arrays.sort(candidates);
    //dfs
    dfs_sum(candidates, 0, target, path, res);

    return res;
  }

  public void dfs_sum(
    int[] candidates,
    int begin_node_idx,
    int target_sum,
    List<Integer> path,
    List<List<Integer>> res
  ) {
    for (int i = begin_node_idx; i < candidates.length; i++) {
      int next_val = target_sum - candidates[i];
      if (i > begin_node_idx && candidates[i] == candidates[i - 1]) { //和39题的区别1
        continue;
      }
      if (next_val == 0) {
        path.add(candidates[i]);
        res.add(new ArrayList<Integer>(path)); //path是引用变量，所以要新申请
        path.remove(path.size() - 1); //回溯
        return;
      } else if (next_val < 0 || i == candidates.length - 1) { //和39题的区别2
        return;
      } else {
        path.add(candidates[i]);
        dfs_sum(candidates, i + 1, next_val, path, res); //和39题的区别3
        path.remove(path.size() - 1); //回溯
      }
    }
  }
}

42. 接雨水⁍

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

img

1
2
3
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

思路一：动态规划 1ms,81.65%,38.2MB

对于下标$i$，下雨后水能到达的最大高度等于下标$i$两边的最大高度的最小值，下标处能$i$接的雨水量等于下标$ i$ 处的水能到达的最大高度减去$ height[i]$

  • $leftMax[i]$：记录i左边的最大高度，实时更新；$leftMax[i]=max(leftMax[i-1], height[i])，1<=i<=n-1$
  • $rightMax[i]：$记录i右边的最大高度，实时更新；$rightMax[i]=max(rightMax[i+1],height[i]) 0<=i<=n-2$
  • 包含自己，如果左右两边都是自己最大，就说明i处凸了出来
  • 最终$i处的雨水量=min(leftMax[i],rightMax[i])-height[i]$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {

  public int trap(int[] height) {
    int s = 0;
    int n = height.length;
    int[] leftMax = new int[n];
    int[] rightMax = new int[n];

    leftMax[0] = height[0];
    rightMax[n - 1] = height[n - 1];

    for (int i = 1; i < n; i++) {
      leftMax[i] = Math.max(leftMax[i - 1], height[i]);
      rightMax[n - i - 1] =
        Math.max(rightMax[n - i - 1 + 1], height[n - i - 1]);
    }

    for (int i = 0; i < n; i++) {
      s += Math.min(leftMax[i], rightMax[i]) - height[i];
    }

    return s;
  }
}

思路二：单调栈 接雨水 - 接雨水 - 力扣（LeetCode） (leetcode-cn.com)

思路三：双指针 只需要O(1)的空间复杂度

维护两个指针 $\textit{left}$ 和 $\textit{right}$，以及两个变量 $\textit{leftMax}$ 和 $\textit{rightMax}$，

初始时 $\textit{left}=0,\textit{right}=n-1,\textit{leftMax}=0,\textit{rightMax}=0$。

指针 $\textit{left}$ 只会向右移动，指针 $\textit{right}$ 只会向左移动，在移动指针的过程中维护两个变量 $\textit{leftMax}$ 和 $\textit{rightMax}$ 的值。

当两个指针没有相遇时，进行如下操作：

使用 $\textit{height}[\textit{left}]$和 $\textit{height}[\textit{right}]$的值更新 $\textit{leftMax}$ 和 $\textit{rightMax}$ 的值；

  • 如果 $\textit{height}[\textit{left}]<\textit{height}[\textit{right}]$，则必有 $\textit{leftMax}<\textit{rightMax}$，

    下标 $\textit{left}$ 处能接的雨水量等于 $\textit{leftMax}-\textit{height}[\textit{left}]$，

    将下标 $\textit{left}$ 处能接的雨水量加到能接的雨水总量，然后将 $\textit{left}$ 加 1（即向右移动一位）；

  • 如果 $\textit{height}[\textit{left}] \ge \textit{height}[\textit{right}]$，则必有 $\textit{leftMax} \ge \textit{rightMax}$，

    下标 $\textit{right}$ 处能接的雨水量等于 $\textit{rightMax}-\textit{height}[\textit{right}]$，

    将下标 $\textit{right}$ 处能接的雨水量加到能接的雨水总量，然后将 $\textit{right}$ 减 1（即向左移动一位）。

当两个指针相遇时，即可得到能接的雨水总量。

48. 旋转图像⁍

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

img

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

思路：

分两步：

  1. 沿右斜对角线’\'翻转
    1. swap(M[i][j],M[j][i])
  2. 沿垂直中轴线’|'翻转
    1. swap(M[i][j],M[i][n-1-j])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {

  public void rotate(int[][] matrix) {
    int n = matrix.length;
    for (int i = 0; i < n; i++) {
      for (int j = i + 1; j < n; j++) {
        swap(matrix, i, j, j, i);
      }
    }
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < n / 2; j++) {
        swap(matrix, i, j, i, n - 1 - j);
      }
    }
  }

  public void swap(int[][] matrix, int x0, int y0, int x1, int y1) {
    int tmp = matrix[x0][y0];
    matrix[x0][y0] = matrix[x1][y1];
    matrix[x1][y1] = tmp;
  }
}

53. 最大子数组和⁍

Tags
Companies

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

1
2
3
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

思路一：动态规划

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {

  public int maxSubArray(int[] nums) {
    int maxs = nums[0];
    int s = 0; //前缀和
    for (int i : nums) {
      s = Math.max(s + i, i); //如果i更大就是i的值，相当于把下面的负数情况加了进去
      maxs = Math.max(s, maxs);
    }

    return maxs;
  }

⭐思路二：分治

定义操作：get(a,l,r) 表示查询 a 序列 [l,r] 区间内的最大子段和

目标函数：get(nums, 0, nums.length - 1)

对于一个区间 $[l,r]$，我们取 $m = \lfloor \frac{l + r}{2} \rfloor$，对区间 $[l,m]$ 和 $[m+1,r]$ 分治求解。

  • 对于一个区间 $[l,r]$，我们可以维护四个量：

    $\textit{lSum}$ 表示 $[l,r]$ 内以 l 为左端点的最大子段和
    $\textit{rSum}$ 表示 $[l,r]$ 内以 r 为右端点的最大子段和
    $\textit{mSum}$ 表示 $[l,r]$ 内的最大子段和
    $\textit{iSum}$ 表示 $[l,r]$ 的区间和

  • 以下简称 $[l,m]$ 为 $[l,r]$ 的「左子区间」，$[m+1,r]$ 为 $[l,r]$ 的「右子区间」。我们考虑如何维护这些量呢（如何通过左右子区间的信息合并得到 $[l,r]$ 的信息）？

  • 对于长度为 $1$ 的区间 $[i, i]$，四个量的值都和 $\textit{nums}[i]$ 相等。

  • 对于长度大于 $1$ 的区间：首先最好维护的是 $\textit{iSum}$，区间 $[l,r]$ 的 $\textit{iSum}$ 就等于「左子区间」的 $\textit{iSum}$ 加上「右子区间」的 $\textit{iSum}$。

    • 对于 $[l,r]$ 的 $\textit{lSum}$，存在两种可能，它要么等于「左子区间」的 $\textit{lSum}$，要么等于「左子区间」的 $\textit{iSum}$ 加上「右子区间」的 $\textit{lSum}$，二者取大。
    • 对于 $[l,r]$ 的 $\textit{rSum}$，同理，它要么等于「右子区间」的 $\textit{rSum}$，要么等于「右子区间」的 $\textit{iSum}$ 加上「左子区间」的 $\textit{rSum}$，二者取大。
    • 当计算好上面的三个量之后，就很好计算 $[l,r]$ 的 $\textit{mSum}$ 了。我们可以考虑 $[l,r]$ 的 $\textit{mSum}$ 对应的区间是否跨越 $m$——它可能不跨越 $m$，也就是说 $[l,r]$ 的 $\textit{mSum}$ 可能是「左子区间」的 $\textit{mSum}$ 和 「右子区间」的 $\textit{mSum}$ 中的一个；它也可能跨越 $m$，可能是「左子区间」的 $\textit{rSum}$ 和 「右子区间」的 $\textit{lSum}$ 求和。三者取大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {

  public class Status { // 维护四个量
    public int lSum, rSum, mSum, iSum;

    public Status(int lSum, int rSum, int mSum, int iSum) {
      this.lSum = lSum;
      this.rSum = rSum;
      this.mSum = mSum;
      this.iSum = iSum;
    }
  }

  public int maxSubArray(int[] nums) {
    return getInfo(nums, 0, nums.length - 1).mSum;
  }

  public Status getInfo(int[] a, int l, int r) {
    if (l == r) { //递归终止条件
      return new Status(a[l], a[l], a[l], a[l]);
    }
    int m = (l + r) >> 1; //右移1，相当于➗2
    Status lSub = getInfo(a, l, m);
    Status rSub = getInfo(a, m + 1, r);
    return pushUp(lSub, rSub); // 更新两个的量
  }

  public Status pushUp(Status l, Status r) { //维护这些量
    int iSum = l.iSum + r.iSum;
    int lSum = Math.max(l.lSum, l.iSum + r.lSum);
    int rSum = Math.max(r.rSum, r.iSum + l.rSum);
    int mSum = Math.max(Math.max(l.mSum, r.mSum), l.rSum + r.lSum);
    return new Status(lSum, rSum, mSum, iSum);
  }
}

55. 跳跃游戏⁍

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

思路一 动态规划

很慢。。

思路二 贪心算法

如果 最远可以到达的位置 大于等于数组中的最后一个位置，那就说明最后一个位置可达

  • $maxF$：整个数组最远到的地方，随遍历更新
    • 初始为0
  • $far$： 从下标$i$位置最远能到的地方
    • 先判断$i$是否可达，$maxF>=i$
    • $far=nums[i]+i$
  • 终止：$maxF>=nums.length-1$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {

  public boolean canJump(int[] nums) {
    int MaxF = 0;
    for (int i = 0; i < nums.length; i++) {
      if (MaxF >= i) {
        int far = nums[i] + i;
        MaxF = Math.max(MaxF, far);
        if (MaxF >= nums.length - 1) {
          return true;
        }
      }
    }
    return false;
  }
}

56. 合并区间⁍

主要是要熟悉java的数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {

  public int[][] merge(int[][] intervals) {
    // int n = intervals.length;
    //排序
    Arrays.sort(intervals, (a, b) -> a[0] - b[0]); //lamda表达式
    //可变数组
    List<int[]> res = new ArrayList<int[]>();
    // res.add(intervals[0]);
    for (int i = 0; i < intervals.length; i++) {
      int left = intervals[i][0];
      int right = intervals[i][1];
      //因为排序了，所以left>=INTV[0]
      if (res.size() == 0 || left > res.get(res.size() - 1)[1]) {
        res.add(new int[] { left, right });
      } else {
        res.get(res.size() - 1)[1] =
          Math.max(res.get(res.size() - 1)[1], right);
      }
    }
    return res.toArray(new int[res.size()][]);
  }
}

59. 螺旋矩阵 II⁍

Category Difficulty Likes Dislikes
algorithms Medium (78.30%) 552 -
Tags
Companies

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

img

1
2
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

思路

  • 定义→↓←↑的操作，注意每个操作的转折点
  • 定义loop表示转了一圈，注意loop增加的地方
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {

  public int[][] generateMatrix(int n) {
    int loop = 1;
    int[][] mat = new int[n][n];
    int i = 0;
    int j = 0;
    mat[0][0] = 1;

    for (int k = 1; k < n * n; k++) {
      if (j == loop - 1 && i == loop) {
        loop++;
      }
      if (i == loop - 1 && j < n - loop) { //向右
        mat[i][++j] = k + 1;
      } else if (j == n - loop && i < n - loop) { //向下
        mat[++i][j] = k + 1;
      } else if (i == n - loop && j > loop - 1) { //向左
        mat[i][--j] = k + 1;
      } else if (j == loop - 1 && i > loop) { //向上
        mat[--i][j] = k + 1;
      }
    }
    return mat;
  }
}

79. 单词搜索⁍

Tags
Companies

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

img

1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

思路： 递归+剪枝

  • 如果 $\textit{board}[i][j] \neq s[k]$，当前字符不匹配，直接返回 $\texttt{false}$。
  • 如果当前已经访问到字符串的末尾，且对应字符依然匹配，此时直接返回 $\texttt{true}$。否则，遍历当前位置的所有相邻位置。
  • 如果从某个相邻位置出发，能够搜索到子串 $word[k+1…]$，则返回 $\texttt{true}$，否则返回 $\texttt{false}$。

这样，我们对每一个位置 $(i,j)$ 都调用函数 $\text{check}(i, j, 0)$ 进行检查：只要有一处返回 $\texttt{true}$，就说明网格中能够找到相应的单词，否则说明不能找到

  • 额外维护一个与 $board$ 等大的 $visited$ 数组，来标记是否访问过（记得回溯时将$\texttt{false}$的部分重置回未访问过）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    // 四个方向
    final int[][] directions = {{0, 1},{0, -1},{1,0},{-1,0}};
    int m,n;
    public boolean exist(char[][] board, String word) {
        m = board.length;
        n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                boolean res = backtracking(board, word, i, j, 0, visited); // 先找第一个
                if (res) {
                    return true;
                }
            }
        }
        return false;
    }

    public boolean backtracking(char[][] board, String word, int i, int j, int k, boolean[][] visited){
        // i,j 代表网格坐标，k代表遍历到第几个字符

        boolean result = false;
        // 终止条件1：字符串遍历到头
        if (k >= word.length()) {
            return true;
        }
        // 终止条件2：坐标不合法
        if (i<0||i>=m||j<0||j>=n) {
            return false;
        }

        // 终止条件3：当前格子访问过
        if (visited[i][j]) {
            return false;
        }
        // 终止条件4：当前网格不满足题意
        if (word.charAt(k) != board[i][j]) {
            return false;
        } else {
            visited[i][j] = true; // 已访问
            result = true;
        }
        // 遍历各个方向
        for (int[] direction:directions) {
            int new_i = i + direction[0];
            int new_j = j + direction[1];
            result = backtracking(board, word, new_i, new_j, k + 1, visited);
            if (result) {
                break;
            }
        }
        visited[i][j] = false;
        return result;
    }
}

84. 柱状图中最大的矩形⁍

Tags
Companies

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

img

1
2
3
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

思路

  • 对于元素$n[i]$，要找到$i$左边第一个<=它的数和右边第一个<=它的数

    • 维护$left[i]$和$right[i]$，分别是i左边第一个<=它的数和右边第一个<=它的数，则

      $$area[i]=((right[i]-1)-(left[i]+1)+1)\times n[i]$$

  • 维护一个单调栈，栈底到栈顶的存的下标对应的元素单增，遍历数组，每次遇到n[i]时，就与n[top]比较

    • 循环，将>=n[i]的top出栈，全pop完之后
      • $left[i]=top$
      • 特例：栈为空，则$left[i]=0-1=-1$
      • push(i)
    • 对于每个pop操作
      • $right[top]=i$
    • 遍历到头之后，将栈内的所有元素都Pop出去，此时
      • $right[top]=n$

  • 最后计算最大面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {

  public int largestRectangleArea(int[] heights) {
    int n = heights.length;
    int[] left = new int[n];
    int[] right = new int[n];

    LinkedList<Integer> stack = new LinkedList<>();
    for (int i = 0; i < n; i++) {
      while (!stack.isEmpty() && heights[i] <= heights[stack.peekLast()]) {
        //执行一次Pop
        int top = stack.pollLast();
        right[top] = i;
      }
      left[i] = stack.isEmpty() ? -1 : stack.peekLast();
      stack.add(i);
    }
    while (!stack.isEmpty()) {
      int top = stack.pollLast();
      right[top] = n;
    }
    int ans = 0;
    for (int i = 0; i < n; i++) {
      ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
    }
    return ans;
  }
}
  • left[i]: 左数最接近的一个<=height[i]的数的下标，起始为-1
  • right[i]：右数最接近的一个<=height[i]的数的下标，起始为n
  • 则实际的长度为（right[i]+left[i]-1）
  • 面积则为height[i]*（right[i]+left[i]-1）

581. 最短无序连续子数组⁍

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的 最短 子数组，并输出它的长度。

思路

  1. 从左往右找到第一个不满足单调增的数下标i+1；从右往左找到第一个不满足单调减的数下标j-1
  2. 则左边最大值就是nums[i]，右边的最大值就是nums[j]
  3. 在区间[i,j]中，遍历，更新最大Max和最小Min
  4. 找左边第一个比Min大的数和右边第一个比Max小的数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def findUnsortedSubarray(self, nums: List[int]) -> int:
        i = 0
        j = len(nums)-1
        while i < len(nums)-1 and nums[i]<=nums[i+1]:
            i+=1
        
        # 考虑特殊情况
        if i == len(nums)-1:
            return 0

        while j > 0 and nums[j]>=nums[j-1]:
            j-=1
        
        Max = nums[i]
        Min = nums[j]

        # 在i，j区间内找最大和最小值
        for num in nums[i:j]:
            Max = max(num, Max)
            Min = min(num, Min)


        # 找到左边第一个比Min大的数
        left = 0
        while left < i and nums[left] <= Min:
            left+=1
        # 找到右边第一个比Max小的数
        right = len(nums) - 1
        while right > j  and nums[right] >= Max:
            right-=1
        
        return right-left+1

⭐560. 和为 K 的子数组⁍

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的连续子数组的个数。

思路

区间和–》前缀和

  • 定义 prefixSum 数组，prefixSum[x]：第 0 项到 第 x 项 的和。
    $$prefixSum[x] = nums[0] + nums[1] +…+nums[x]$$
  • nums 的某项 = 两个相邻前缀和的差：
    $nums[x] = prefixSum[x] - prefixSum[x - 1]$
  • nums 的 第 i 到 j 项 的和，有：
    $$nums[i] +…+nums[j]=prefixSum[j] - prefixSum[i - 1]$$

当 i 为 0，此时 i-1 为 -1，我们故意让 prefixSum[-1] 为 0，使得通式在i=0时也成立：
$nums[0] +…+nums[j]=prefixSum[j]$

不用求出 prefixSum 数组

其实我们不关心具体是哪两项的前缀和之差等于k，只关心 等于 k 的前缀和之差出现的次数c ，就知道了有c个子数组求和等于k。

  • 遍历 nums 之前，我们让 -1 对应的前缀和为 0，这样通式在边界情况也成立。即在遍历之前，map 初始放入 0:1 键值对（前缀和为0出现1次了）。

  • 遍历 nums 数组，求每一项的前缀和，统计对应的出现次数，以键值对存入 map。

  • 边存边查看 map，如果 map 中存在 key 为「当前前缀和 - $k$」，说明这个之前出现的前缀和，满足「当前前缀和 - 该前缀和 == $k$」，它出现的次数，累加给 count。

链接：https://leetcode-cn.com/problems/subarray-sum-equals-k/solution/dai-ni-da-tong-qian-zhui-he-cong-zui-ben-fang-fa-y/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        cnt = 0
        preSum = 0
        myMap = {}
        myMap[0] = 1
        for num in nums:
            preSum += num
            if preSum - k in myMap:
                cnt += myMap[preSum-k]
            if preSum not in myMap:
                myMap[preSum] = 1
            else:
                myMap[preSum] += 1

        return cnt

  1. 代码随想录-二分查找 (programmercarl.com) ↩︎

  2. 代码随想录-数组理论基础 (programmercarl.com) ↩︎

  3. 代码随想录-数组总结篇 (programmercarl.com) ↩︎ ↩︎ ↩︎